近日,《物理评论研究》(Physical Review Research)发表题为Split-ring polariton condensates as macroscopic two-level quantum systems的研究论文。西湖大学国际极化基元中心主任、物理讲席教授AlexeyKavokin和该中心研究员Igor Chestnov同为通讯作者,作者Evgeny Sedov也来自该中心。
A research article namedSplit-ring polariton condensates as macroscopic two-level quantum systemsappearedrecentlyin Physical Review Research (PRR). Alexey Kavokin, Chair Professor of Physics, director of International Center of Polaritonics (ICP) of Westlake University, together with Igor Chestnov from ICP are the correspondent authors. Evgeny Sedov is another author from ICP.
Kavokin、Chestnov和合作者提出,一个极化激元凝聚的开环系统可以作为量子计算平台。这一新型平台具有全光控制带来的可规模化、操作温度可接近室温、易与传统微电子器件整合等多个优点。在文章中,研究人员描述了这一新型平台中量子比特的设计和性能,提出了单比特和双比特量子门的理论模型,并给出了实现量子算法的协议。
Kavokin, Chestnov and collaborators proposed that the split-ring condensates of exciton-polaritons can serveas a new platform for quantum computation. The advantages of this new platform are in its high scalability ensured by the optical control, high operation temperature (up to room temperature) and integrability with classical microelectronic devices. In the article, they described the design of the proposed qubit and its figure of merit, the implementations of single- and double- qubit quantum gates, and a protocol for the realization of a practical quantum algorithm.
实现量子计算的多条路径
Promisingpaths to the ultimate quantum computing
量子计算处于新一轮科技革命和产业革命的前沿。诸多国家投入大量资源,推动从多条路径发展量子计算。未来的量子计算究竟是在什么平台,以什么材料实现,还是一个未解之谜。近年来,以超导电路、冷原子、离子、纯光学系统为平台的主流路径,已经取得了巨大的发展。
Quantum computing is at the frontier of new Sci-tech revolution and industrial transformation. Many nations have invested a lot of resources in the development of quantum computing with various approaches. It is still unclear which material platform is the most suitable for the realization of future quantum computers and simulators. A tremendous progress in the development of quantum technologies is apparent, with superconducting circuits,cold atomsinopticaltraps, ions, purelyphotonicssystems.
以半导体材料为平台的研究人员正在奋力追赶,目前已能用量子点产生单光子源,且在纳米结构上实现了量子计算。运用半导体材料加工的微腔中,一种准粒子(极化激元)也可用来实现量子计算。
Researchers working with semiconductor platforms are catching up. In this regard, a remarkable progress has recently been achieved with quantum computing in semiconductor nanostructures as well as in the creation of single-photon sources based on quantum dots. On top of that, semiconductor microcavities hosting ensembles of quasiparticles (polaritons) have shown a high potentiality of realizing quantum computing.
基于极化激元来实现量子计算,有众多优势。但是,人们至今从未实现用极化激元来搭建一个量子比特。
Using polaritons to realize quantum computing has many advantages. Yet, a polariton qubit has never been convincingly demonstrated till now.
类比磁通量子比特,构建极化激元量子比特
Construct a polariton quantum bit analog to a flux quantum bit
Kavokin、Chestnov和合作者提出了用极化激元来构建一个量子比特的设想。他们发现,极化激元中的超流与超导电路中的电流本质上非常相似。类比超导电路的磁通量子比特,可以搭建一个极化激元的量子比特。
Kavokin, Chestnov and collaborators proposed an approach to construct a polariton quantum bit (qubit). They found a strong fundamental similarity of superfluid polariton flows and superconducting electric currents. They exploited this similarity to build a polariton analogue of the superconducting flux qubit.
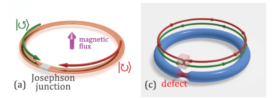
图1左图:超导磁通量子比特;右图:与开环极化激元量子比特。
Fig1 A superconducting flux qubit (left) and a split-ring polariton qubit (right).
表:磁通量比特和开环极化激元比特的类比
Table: Analogy between a superconducting flux qubit (left) and a split-ring polariton qubit (right).
磁通量子比特 A flux qubit |
开环极化激元量子比特 Asplit-ring polariton qubit |
磁通量子比特,是在超导电路中插入约瑟夫森结(Josephson junction) A superconducting flux qubit is a superconducting circuit containing one or several Josephson junctions |
极化激元量子比特,是在超流环中引入势缺 A polariton qubit is a superfluid polariton ring containing one potential defect |
系统产生顺时针和逆时针超导电流,对外加的磁通量进行抵消或补充,使得总磁通量满足量子化条件 The system is forced to generate clockwise or anti-clockwise currents to either reduce the magnetic flux to zero or to build it up to a full-quantum flux |
系统产生顺时针和逆时针超流,对缺陷引入的相位差进行抵消或补充,使得绕环总相位为0或2π The system is forced to generate clockwise or anti-clockwise superfluid currents to either recede the phase variation to zero or build it up to 2π |
超导电流的对称与反对称组合,构成磁通量子比特的0和1的叠加 The symmetric and anti-symmetric combinations of the superconducting currents form the superposition of qubit 0 and 1. |
超流的对称组合和反对称组合,构成了极化激元量子比特的0和1的叠加 The symmetric and antisymmetric combinations of polariton circular currents form the superposition of qubit 0 and 1. |
实现极化激元量子比特
Realization of a polariton qubit
半导体微腔中,光与物质的强耦合形成了极化激元超流。要在超流环上引入一个势陷,既可以从结构入手(比如在半导体上做刻蚀),也可以通过把泵浦激光空间调制为C字形来实现(如图2左)。前者能够更好地极化激元,而后者通过全光控制调节更为灵活,不需要每次都长新的半导体样品。如此引入势陷,极化激元超流环就好似一个超导通量量子比特。
In semiconductor microcavities, the strong coupling of cavity photons and quantum-well excitons results in superfluid polaritons. To introduce a potential defect in circular superfluid, one could implement structurally (e.g., etch the semiconductor), or by means of a spatially C-shape laser pumping (Fig 2, left). The former has a better spatial localization, while the latter has a full optical control and thus a larger control flexibility without the need to grow a new sample at each geometry change. By doing so, it reproduces the behavior of a superconducting flux qubit.
研究者计算了在时刻零打开C字形泵浦激光后极化激元凝聚角动量的振荡(图2右),这相当于找到了这个多体两能级量子系统的“指纹”。可以看到,这一振荡十分稳定,这是由于这里的环超流态受到了拓扑保护。
To characterize the non-stationary circular currentstates of the condensate, researchers calculated the oscillatory dynamics of the angular momentum, when the split-ring polariton condensateis pumped with the C-shape laser starting from time zero (Fig. 2, right). The harmonic oscillations of the angular momentum of thecondensate can be considered as a fingerprint of a many-bodytwo-level quantum system. The reason of the surprising stability of oscillations is inthe topological protection of circular current states in split-ringcondensates.
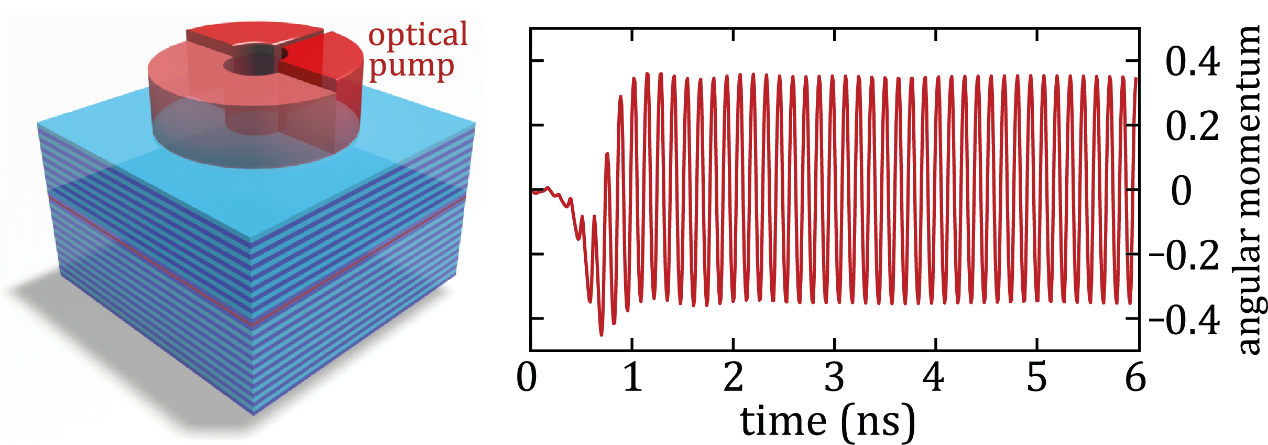
图2用空间调制成C字形泵浦来半导体(左)。从零时刻开始泵浦,计算所得平均角动量m随时间的演化。
Fig 2 The semiconductor is pumped with a C-shape spatially modulated laser (left). Theaverageangularmomentum of the condensate after the pumping laser is switched on at time zero(right).
通过控制非谐振泵浦的强度,研究者可将这个开环极化激元比特设置到量子态0或1(图3)。 研究者发现这种两能级系统用来做量子比特,鲁棒性非常好。以典型的GaAs半导体微腔结构为例,这里的相干时间超过100ns,这比单个极化激元的寿命长(6ps),也比凝聚的相干时间要长(几个ns)。如果进一步改进微腔样品的品质,对系统参数进行微调,相干时间有往达到毫秒量级。由此估算,逻辑操作可以达到125ps,佳度(figure of merit)超过1000,可与目前最好的超导量子比特相媲美。
By controlling the intensity of the nonresonant pump laser, one can set the split-ring polaritonqubitto 0 or 1 (Fig 3). One can see that polariton split-ring condensates demonstratethe properties of robust two-level systems and can be consideredas qubits. For a conventional GaAs-based microcavity, the coherence time exceeds 100ns. This ismuch beyond the single polariton lifetime (as short as 6 ps) and even beyond the coherence time of the condensateas a whole (a few ns). With a further improvement of the microcavitysample’s quality and tuning the system parameters onecan expect an extension of the coherence times up to the millisecondrange. Thus, estimating the single logic operation time by the periodof the oscillations on the Bloch sphere that is of the orderof 125 psin this case, one can estimate the figure of merit of a polariton qubit to be morethan 103, that matches those of best superconducting qubits.
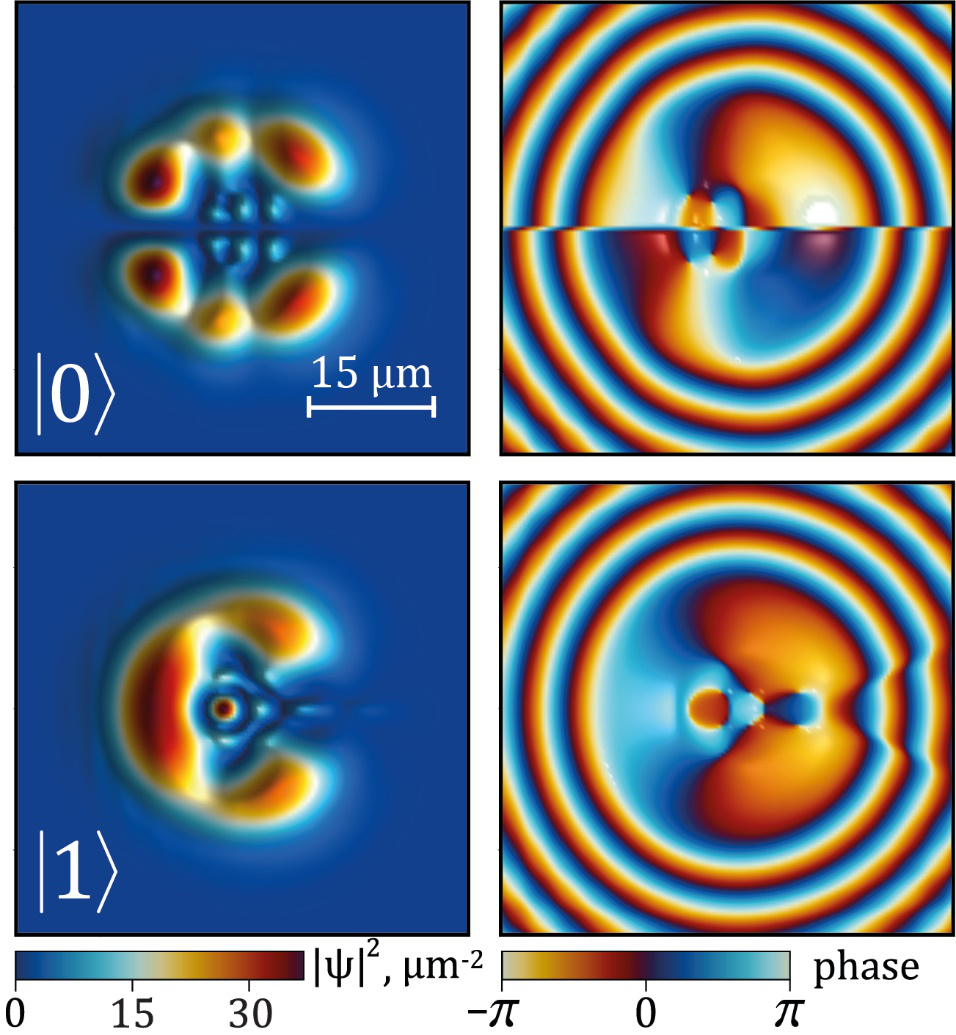
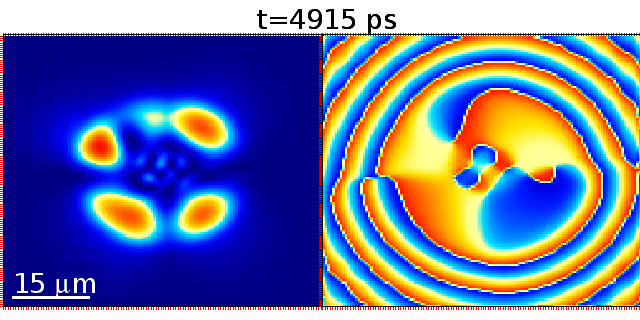
图3量子比特处于0和1时,开环极化激元波函数的密度(左)和相位(右)。动态振荡见下方视频。
Fig 3 The density and phase of the two states of the split-ring polariton qubit.. The full dynamics of the oscillations is shown in the video below.
从单比特到多比特
From single qubit to multiplequbits
单个半导体微腔可以作为一个量子比特。同轴叠起两个微腔,可以是耦合的两个量子比特(图4左)。
Single semiconductor cavity works as a single qubit. Two of them coaxially stacked form two coupled qubits.
这两个量子比特可以是相对独立的。将两个微腔的禁带设置到不同位置,就可以分别激发和读取单个比特;而通过外接电极产生的辐射电场以及外加垂直磁场,可以有选择地调节量子比特的能带隙,由此达成单个比特的控制。
These two qubits arerelativelyindependent, in the sense that they can be selectively controlled. Different positions of stop-bands of the two cavities allow for the selective non-resonant excitation and read-out of the qubits. With the radial electric field generated by the electrodes and a perpendicular external magnetic field, one can selectively tune the qubits energy gap.
这两个量子比特又是可以合作的。和变压器的工作原理类似,一个比特的超流的感生磁场影响到另一个比特,由此达成两个比特之间的耦合。
These two qubits work together, as they are mutually coupled. The magnetic field induced by the superfluid of one qubit affects the other qubit, in the same fashion as an inductive coil acts in an electric transformer.
通过设计这样一对开环极化激元,研究人员还探究了用两个量子比特来实现比特交换(iSWAP)协议(图4中)。研究人员还进一步模拟用一个量子系统来实现道奇算法(Deutsch’s algorithm),根据计算,平均出错率仅为几个百分点(图4右)。
Designing a pillar microcavity structure that sustains a couple of split-ring polariton condensates, Kavokin, Chestnov and collaborators proposed schemes for the implementation of the iSWAP two-qubit gate (Fig 4 middle). Further, they simulated the implementation of the Deutsch’s algorithm with a polariton quantum network based on single- and double-qubit gates, having the average error within few percent (Fig 4 right).
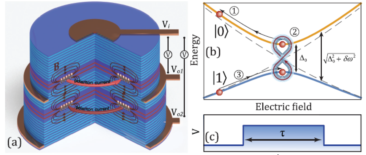

图4两个量子比特的模型(左);两比特门实现比特交换(中),道奇算法的实施和保真度估算(右)
Fig 4 Two-qubit prototype (left); A protocol for the implementation of an iSWAP two-qubit gate (middle); Implementation of the Deutsch’s algorithm(right).
开辟量子计算的新路径
Apromising new path towards quantum computing
Kavokin、Chestnov及合作者用开环结构的极化激元设计了一个极具发展前景的量子系统。它不仅具有有非常高的佳值。并且由于它基于半导体技术,因而具有可规模化、高操作温度、易与传统半导体器件整合等优势。它为最终实现使用的量子计算,开辟了一条新的路径。
Kavokin,Chestnov and collaborators demonstrated a high potentiality of polariton quantum networks based on split-ring geometry polariton condensates. Polariton qubits have a very high figureofmerit. The evident advantages of the considered quantum system are in its high scalability, high operation temperature, ultrafast logic operations and potential integrability with classical semiconductor based nano-electronic devices.It is a promising new path towards quantum computing.